Leyes de los radicales

Radical es un adjetivo que puede referirse a aquello perteneciente o relativo a la raíz. De las leyes de los exponentes pueden obtenerse ciertas leyes útiles de los radicales. Las leyes de los radicales pueden emplearse para hacer cambios necesarios en los radicales, entre los más comunes están:

1. Remover factores del radicando.

2. Remover el denominador de un radicando.

3. Expresar un radical como un radical de orden más bajo.

4. Incluir un factor dentro de un signo radical. Se dice que su forma más simple es cuando se han llevado a cabo, y hasta donde es posible, las operaciones 1, 2 y 3.

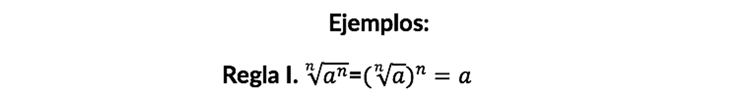
Cuando un número está dentro de un radical y a su vez está elevado a la misma potencia del radical, como resultado se tendrá sólo el número.

Cuando en la raíz no se encuentre indicado algún número, se supondrá que es raíz cuadrada. Se puede convertir el radical a fracción colocando el exponente de la base como numerador, y el número del radical, pasa a ser denominador de la fracción, obteniéndose:

Se descompone en factores el

de tal forma que alguno de ellos tenga raíz cuadrada. 

Una raíz de una fracción, se puede distribuir en el numerador denominador, por lo tanto, la raíz cúbica de la fracción se puede separar como la raíz cúbica de 27 y raíz cúbica de 8. Posteriormente se puede simplificar reacomodando los números de tal forma puedan tener raíz cúbica.

Reacomodamos los números dentro del radical como:

Cuando un radical se encuentre dentro de otro, se pueden multiplicar entre ellos para simplificarlo a uno solo.